CUPED로 A/B 테스트를 더 빠르고 정확하게

---

A/B 테스트

A/B 테스트란 사용자 경험을 개선하기 위해 두 가지 이상의 옵션들을 비교하여 최적의 선택을 도출하는 실험 설계 기법이다. 데이터 분석 환경이 갖추어진 많은 회사들이 UI 혹은 알고리즘을 개선하고자 A/B 테스트를 적극적으로 활용하고 있다.

통계학에서는 가설 검정이란 이름으로 더 잘 알려져 있는데, 온라인 실험 환경에서 데이터 기반 의사결정을 목적으로 수행할 때 특별히 A/B 테스트라고 부르는 듯 하다.

이해를 돕기 위하여 웹 사이트에서 버튼 색상을 변경했을 때 클릭률(Click-Through Rate, CTR)에 어떤 영향을 미치는지 분석하는 상황을 가정해보자.

유형	설명	표본 수	CTR
대조군(A)	흰색 배경에 회색 버튼	100	13%
실험군(B)	흰색 배경에 빨간색 버튼	100	15%

실험 결과, 빨간색 버튼의 CTR이 회색 버튼보다 높으므로 우리는 버튼 색깔을 빨간색으로 교체하기로 결정할 수 있다.

---

p-value

하지만 이렇게 결론 내려도 문제가 없는걸까? 다시 의사결정 과정으로 되돌아가보자.

기존에는 회색 버튼을 사용하고 있었기 때문에 최악의 상황은 버튼 색깔을 교체했음에도 불구하고 CTR이 감소하는 것이다. 따라서 우리는 긍정이라 판단했지만 실제론 아닌 경우(False Positive, FP)에 유의하여 의사결정을 해야 했다.

결정\실제	CTR 상승	CTR 유지	CTR 감소
색깔 유지(N)	-	당연함(TN)	-
색깔 교체(P)	뿌듯함(TP)	아쉬움(FP)	최악(FP)

다행히도 고등학교에서 이를 1종 오류라고 정의하고 정량적으로 측정할 수 있는 수단을 배웠었는데, 바로 p-value이다. p-value는 실험군의 데이터가 대조군의 분포로부터 관측될 확률을 의미한다.

p-value가 높을수록 실험군의 통계값을 신뢰하기 어렵기 때문에, 실험 전에 미리 정해둔 유의수준을 넘겼다면 실험 결과를 의사결정에 사용하는데 주의를 기울여야 한다.

Python을 이용해 예시에서의 p-value를 계산해보자.

from scipy.stats import binomtest

test = binomtest(k=15, n=100, p=0.13, alternative="greater")
print(f"p-value: {test.pvalue:0.3f}")

[실행 결과]

p-value: 0.317

유의수준을 보통 0.05 ~ 0.10 사이로 설정한다는 점을 고려해보면, 0.317이라는 수치는 너무 높다. 따라서 해당 실험의 결과를 신뢰하기는 어려울 것으로 보인다.

---

z-test

앞선 실험에서는 클릭률을 살펴봤었지만, A/B 테스트에서 표본 집단의 확률 분포가 반드시 Binomial 일리란 법이 없다. 그러나 중심 극한 정리(Central Limit Theorem, CLT) 덕분에 표본 수가 적당히 클 때($n\ge 30$) 표본 평균의 확률 분포를 정규 분포로 가정할 수 있다.

$$\overline{X}\sim N(\mu ,\frac{{\sigma }^2}{n})$$

즉, 모집단의 평균과 분산이 각각 $\mu$, $\sigma$이고 표본 개수가 $n$일 때 표본 평균의 통계량은 다음과 같이 정의되며

$$\overline{X}=\frac{\sum X_i}{n}$$

$\overline{X}$의 평균과 분산은 다음과 같다.

$${\mu }_{\overline{X}}=\mu$$ $${\sigma }_{\overline{X}}^2=\frac{{\sigma }^2}{n}$$

이 가정 하에 z-test를 수행하면 다음과 같은 결과를 얻는다.

$$Z=\frac{\overline{X}-\overline{\mu }}{\overline{\sigma }}$$

from scipy.stats import norm

n = 100
mean = 0.13
std = (1/n * 0.13 * (1-0.13)) ** 0.5
z_score = (0.15 - mean) / std

p_value = 1 - norm.cdf(z_score)
print(f"p-value: {p_value:0.3f}")

[실행 결과]

p-value: 0.276

---

t-test

A/B 테스트에서 모집단의 확률 분포를 모르는 경우가 많다. 이땐 어쩔 수 없이 표본집단으로부터 모집단의 모수를 추정할 수 밖에 없는데, 이를 추정량(estimator)이라고 부른다. 그리고 그 기대값이 모집단의 모수와 같은 경우인 불편추정량(unbiased esimator)를 주로 사용한다.

표본 평균 $\overline{X}$의 기대값은 다행히 모집단의 평균 $\mu$와 동일하고 표본 분산의 기대값은 모집단 분산의 $\frac{n-1}{n}$ 이므로, 수식을 약간 수정하여 불편추정량을 계산해 낼 수 있다.

$$\hat{\mu }=\overline{X}$$ $${\hat{s}}^2=\frac{\sum (X_i-\overline{X}{)}^2}{n-1}$$

모집단의 분산 대신 추정량을 사용하면 더 이상 정규 분포를 가정할 수 없다. 따라서 모집단의 분산을 모르는 경우에는 t 분포를 사용해야 한다.

$$t=\frac{\overline{X}-{\mu }_{\overline{X}}}{s_{\overline{X}}}$$

from scipy.stats import t

n = 100
mean_a, std_a = 0.13, (1/(n-1) * 0.13 * (1-0.13)) ** 0.5
mean_b, std_b = 0.15, (1/(n-1) * 0.15 * (1-0.15)) ** 0.5

se = (std_a ** 2 + std_b ** 2) ** 0.5
t_score = (mean_b - mean_a) / se
df = n - 1

pvalue = 1 - t.cdf(t_score, df=df)
print(f"p-value: {pvalue:0.3f}")

[실행 결과]

p-value: 0.343

---

Variance

위의 t-test 수식을 놓고 곰곰이 생각해보면 추정량의 표준편차, 즉 표준오차(Standard Error, SE)가 작아질 수록 p-value가 작아진다. 이는 곧 추정량의 분산(표준오차의 제곱)과 p-value가 비례한다는 의미이기도 하다.

표본 수(n)	표준오차(SE)	t-score	…	p-value
↗	↘	↗		↘
↘	↗	↘		↗

결국 유의수준 보다 낮은 p-value를 얻기 위해서는 분산이 작아질 때까지 표본 수가 쌓이길 기다려야 한다. 예시를 통해서도 표본 수를 1000개로 늘렸을 때 p-value가 떨어지는 것을 볼 수 있다.

from scipy.stats import t

n = 1000
mean_a, std_a = 0.13, (1/(n-1) * 0.13 * (1-0.13)) ** 0.5
mean_b, std_b = 0.15, (1/(n-1) * 0.15 * (1-0.15)) ** 0.5

se = (std_a ** 2 + std_b ** 2) ** 0.5
t_score = (mean_b - mean_a) / se
df = n - 1

pvalue = 1 - t.cdf(t_score, df=df)
print(f"p-value: {pvalue:0.3f}")

[실행 결과]

p-value: 0.099

CUPED

우리는 위에서 이론적 배경을 토대로 표본 수가 많아질 수록 p-value가 감소하는 것을 알 수 있었다. 하지만 A/B 테스트가 실제로 진행되는 온라인 환경에서는 표본 수가 쌓일 때까지 마냥 기다릴 수만은 없다. 실험군과 대조군의 차이를 민감하게 잡아내지 못하면 다음과 같은 문제들이 발생할 수 있기 때문이다.

1. 부정적인 사용자 경험

만약 신규 기능이 사용자 경험에 부정적인 영향을 끼친다면 A/B 테스트가 길어질 수록 실험군의 이탈이 커질 수 있다.

2. 트래픽 수요 증가

데이터 기반 의사결정 환경에서는 더 많은 실험이 요구된다. 트래픽은 제한되어 있으므로 각 실험 기간이 길어질 수록 허용되는 실험의 개수가 적어져 회전율이 떨어진다.

3. 표본 수에 크게 의존

특정 세그먼트에만 영향을 주는 기능이라면 표본의 크기가 작을 수 있다. 이런 경우 실험 결과를 얻어내는데 시간이 오래 걸리거나 불가능할 수 있다.

---

Improving Sensitivity

그렇다면 어떻게 A/B 테스트의 민감도를 높일 수 있을까? 20213년 Microsoft는 분산을 감소시킴으로써 민감도를 높이는 CUPED(Controlled Using Pre-Existing Data) 방식을 제안하였다.

[논문 링크]

• Improving the Sensitivity of Online Controlled Experiments by Utilizing Pre-Experiment Data

해당 논문은 이전까지의 민감도를 높이는 연구들이 특정 상황에서만 사용 가능함을 지적하면서, 사전 실험 데이터(Pre-Experiment Data)를 활용하여 일반적인 상황에서도 실험 결과의 분산을 줄이고 민감도를 높일 수 있음을 주장하고 있다.

• CUPED는 사전 데이터를 사용해 온라인 실험의 분산을 줄이고 민감도를 크게 향상
• 비사용자 기반 지표와 일부 사전 데이터가 누락된 경우에도 적용 가능
• 사전 실험 데이터를 사용하는 것이 가장 큰 분산 감소를 가져온다는 경험적 결과 소개
• Bing에서 실행된 실제 온라인 실험에서 약 50%의 분산 감소를 보였으며, 이는 트래픽을 두 배로 늘리거나 실험 시간을 절반으로 줄이는 것과 같은 효과
• 최적의 사전 실험 기간 설정과 여러 공변량 활용 등 CUPED를 성공적으로 적용할 수 있도록 가이드 제공

---

Methods

CUPED는 분산의 추정량을 줄이기 위해 다음 두 가지 Monte-Carlo Sampling을 사용한다.

1. Control Variates Method

공변량(Covariate)를 사용하여 분산을 줄이는 방식이다. 논문에서는 앞선 예시와는 다르게 확률 변수의 표기를 $Y$, 공변량의 표기를 $X$로 두고 있음에 유의하자.

$${\hat{Y}}_{cv}:=\overline{Y}-\theta \overline{X}+\theta \mathbb{E}[X]$$

여기서 $\theta$는 상수이고 $\theta \overline{X}+\theta \mathbb{E}[X]$의 기대값은 0이기 때문에 ${\hat{Y}}_{cv}$는 여전히 불편추정량이다.

이제 ${\overline{Y}}_{cv}$의 분산을 계산하고

$$\text{var}({\hat{Y}}_{cv})=\text{var}(\overline{Y}-\theta \overline{X})=\frac{1}{n}(\text{var}(Y)+{\theta }^2\text{var}(X)-2\theta \text{cov}(Y,X))$$

${\overline{Y}}_{cv}$를 최소로 하는 $\theta$를 대입하면

$$\theta =\frac{\text{cov}(Y,X)}{\text{var}(X)}$$

우리는 다음과 같은 식을 얻을 수 있다.

$$\text{var}({\hat{Y}}_{cv})=\frac{\text{var}(Y)}{n}-\frac{\text{var}(Y)}{n}\cdot \frac{\text{cov}(Y,X{)}^2}{\text{var}(Y)\cdot \text{var}(X)}=\text{var}(\overline{Y})(1-\text{cor}(Y,X{)}^2)$$

이때 $\rho =\text{cor}(Y,X)$는 -1과 1 사이의 값을 가지므로,

$$\text{var}({\hat{Y}}_{cv})=\text{var}(\overline{Y})(1-{\rho }^2)\le \text{var}(\overline{Y})$$

결과적으로 우리는 $Y$와 상관 관계가 큰 $X$를 활용하여 더 작은 분산을 가진 ${\hat{Y}}_{cv}$를 p-value 계산에 사용할 수 있다.

2. Stratification Method

표본 집단을 여러 그룹(strata)으로 더 잘게 쪼개어 각 그룹 평균에 대한 weighted sum을 추정량으로 선택한다.

$${\hat{Y}}_{strat}:=\sum _k{w}_k{\overline{Y}}_k$$

이때 $w_k$는 $Y$가 그룹 $k$에 속할 확률, ${\overline{Y}}_k$는 그룹 $k$의 표본 평균이다. 자명하게도 ${\hat{Y}}_{strat}$의 기대값은 $\overline{Y}$와 같으므로 ${\hat{Y}}_{strat}$ 또한 불편추정량이다.

$$\text{var}({\hat{Y}}_{strat})=\sum _k\frac{w_k}{n}{\sigma }_k^2\le \sum _k\frac{w_k}{n}{\sigma }_k^2+\sum _k\frac{w_k}{n}({\mu }_k-\mu {)}^2=\text{var}(\overline{Y})$$

사실 Stratification Method은 Control Variates Method의 특수한 버전이다. 논문은 Control Variates Method의 공변량 $X$를 categorical로 둠으로써 Stratification Method의 추정량을 유도해낼 수 있음을 Appendix에서 보이고 있다.

---

Practice

이제 앞서 설명한 두 방식을 A/B 테스트에 적용하기 위해서 어떤 공변량을 선택해야 할지가 남았다. 논문은 실험 이전의 사전 데이터(pre-experiment data)를 활용하여 분산을 줄일 수 있음을 보인다.

1. Control Variates Method

첫 번째로 실험 시작 이전의 데이터를 사전 데이터로 채택한다. 그런데 만일 실험 데이터에는 포함되어 있지만 사전 데이터에 없는 유저가 존재한다면, Control Variates Method를 적용하긴 어려울 것이다.

2. Stratification Method

이때 사용하는 것이 바로 Stratification Method이다. 사전 데이터에 포함된 유저와 그렇지 않은 유저, 두 그룹으로 나눈다. 그러면 사전 데이터에 포함된 유저 그룹에 대해 공변량이 잘 정의되므로 Control Variates 방식을 적용할 수 있다.

---

Results

논문은 Microsoft의 검색 서비스인 Bing을 통해 CUPED가 실제 온라인 실험에서 효과가 있음을 보였다.

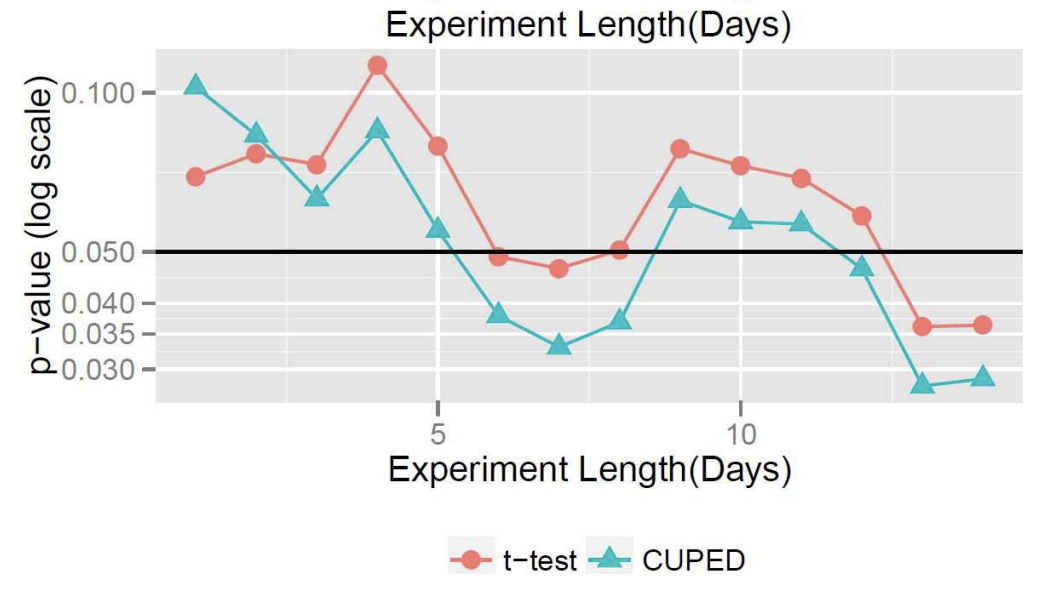
1. p-value

첫번째 그래프는 실험이 진행됨에 따라 t-test와 CUPED 중 어느 p-value가 더 빠르게 유의 수준 아래로 도달하는지 나타내고 있다. 참고로 CUPED는 t-test 보다 유저 수를 절반만 사용했음에도 더 일찍 0.05에 도달하였다.

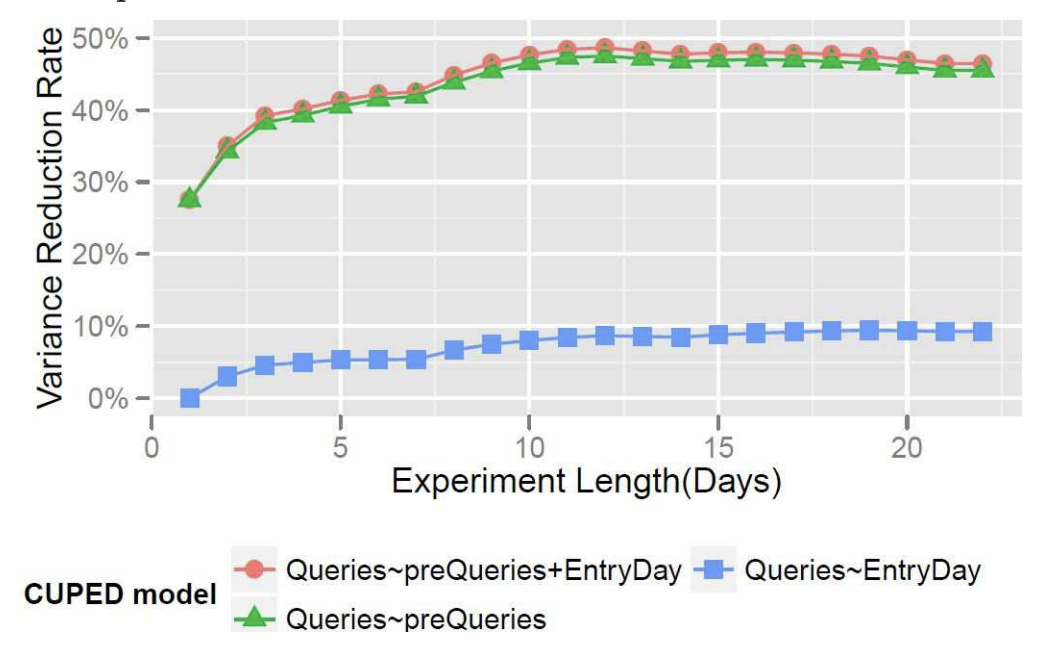
2. Covariate

두번째 그래프는 어떤 공변량을 선택하냐에 따라 분산이 얼마나 감소되는지 보여주고 있다. 사전 데이터를 공변량으로 이용했을 때(preQueries) 가장 차이가 확연히 나타나며, 사용자의 실험 유입 날짜(EntryDay)를 공변량으로 선택하면 비교적 미미한 효과가 나타난다.

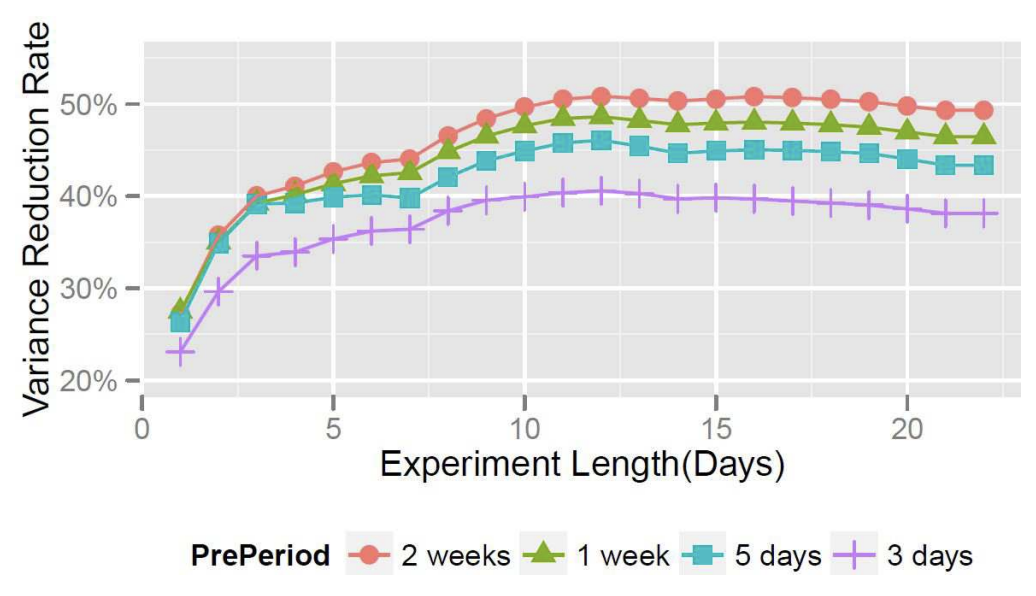
3. Length of Pre-experiment

마지막 그래프는 공변량으로 사용할 사전 데이터의 길이가 분산 감소에 어떤 영향을 미치는지 보여준다. 이를 통해 우리는 2주치의 사전 데이터를 사용했을 때 분산이 약 50% 감소하는 것을 볼 수 있다.

Code

다음 예제를 참고하여 Control Variates Method의 코드를 재구성 해보았다.

• https://github.com/mtrencseni/playground/blob/master/CUPED.ipynb

무작위로 실험 데이터를 생성하였으므로 실행할 때마다 결과가 달라지겠지만, 대부분의 경우 CUPED의 p-value가 더 낮음을 확인할 수 있다.

import numpy as np
from scipy import stats

def get_AB_samples(before_mean, before_sigma, eps_sigma, treatment_lift, N):
    A_before = np.random.normal(loc=before_mean, scale=before_sigma, size=N)
    B_before = np.random.normal(loc=before_mean, scale=before_sigma, size=N)
    A_after  = A_before + np.random.normal(loc=0, scale=eps_sigma, size=N)
    B_after  = B_before + np.random.normal(loc=treatment_lift, scale=eps_sigma, size=N)
    return A_before, B_before, A_after, B_after

def get_cuped_adjusted(A_before, B_before, A_after, B_after):
    cv = np.cov([np.concatenate([A_after, B_after]), np.concatenate([A_before, B_before])])
    theta = cv[0, 1] / cv[1, 1]
    mean_before = np.concatenate([A_after, B_after]).mean()
    A_after_adjusted = A_after - (A_before - mean_before) * theta
    B_after_adjusted = B_after - (B_before - mean_before) * theta
    return A_after_adjusted, B_after_adjusted

def lift(A, B):
    return B.mean() - A.mean()

def p_value(A, B):
    return stats.ttest_ind(A, B, equal_var=False, alternative="less").pvalue

N = 100
before_mean = 130
before_sigma = 30
eps_sigma = 20
treatment_lift = 10

A_before, B_before, A_after, B_after = get_AB_samples(before_mean, before_sigma, eps_sigma, treatment_lift, N)
A_after_adjusted, B_after_adjusted = get_cuped_adjusted(A_before, B_before, A_after, B_after)

print("A mean before = {:.1f}, A mean after = {:.1f}, A mean after adjusted = {:.1f}".format(A_before.mean(), A_after.mean(), A_after_adjusted.mean()))
print("B mean before = {:.1f}, B mean after = {:.1f}, B mean after adjusted = {:.1f}".format(B_before.mean(), B_after.mean(), B_after_adjusted.mean()))
print("Traditional    A/B test evaluation, lift = {:.3f}, p-value = {:.3f}".format(lift(A_after, B_after), p_value(A_after, B_after)))
print("CUPED adjusted A/B test evaluation, lift = {:.3f}, p-value = {:.3f}".format(lift(A_after_adjusted, B_after_adjusted), p_value(A_after_adjusted, B_after_adjusted)))

[실행결과]

A mean before = 129.4, A mean after = 129.4, A mean after adjusted = 131.8
B mean before = 128.2, B mean after = 134.2, B mean after adjusted = 137.8
Traditional    A/B test evaluation, lift = 4.772, p-value = 0.172
CUPED adjusted A/B test evaluation, lift = 5.971, p-value = 0.021